Piccola nota di colore matematico durante la cronaca Rai: il giornalista della Gazzetta dello Sport (non ricordo il nome e me ne scuso) invitato a commentare le prime fasi della cronometro, dimostra le sue abilità matematiche affermando che
Contador sta guadagnando un secondo al chilometro dopo che nei primi 7 Km della crono ha ottenuto un vantaggio di 4"Da che mondo è mondo, però, 4" in 7 Km sono poco più di mezzo secondo al chilometro (0.57, per la precisione). Capisco che il calcoli a mente non siano sempre così semplici da fare, ma in questo caso non mi sembrava poi così difficile dare una valutazione abbastanza corretta della situazione.
Detto questo ritorniamo un attimo allo sport. Al di là delle critiche al fair play per questi due atleti (personalmente il loro comportamento è stato esemplare: fossero tutti così gli atleti a fine gara), o per il troppo tatticismo, alla fine hanno semplicemente dimostrato, sulle montagne, di essere i più forti. In una parola: inarrestabili. Contador, forse, ha fatto un solo errore, non andare a vincere il Tourmalet: ne aveva le forze. In ogni caso i due atleti hanno fatto una buona cronometro, da scalatori che si giocano il Tour oserei dire: forse sono uno dei pochi a ritenere che quest'anno Contador ha fatto una preparazione incentrata sulla montagna piuttosto che sulla cronometro, dove il distacco finale, se non si è specialisti, è una questione di gambe e di concentrazione. Unico difetto, però, è quello di correre per l'Astana (ancora per poco?), squadra finanziata con il petrolio, ovvero quanto di più lontano c'è dalle biciclette.
A questo punto, in attesa dell'arrivo all'ombra della Torre, oggi si andranno ad approfondire alcuni aspetti della meccanica dei fluidi, importanti proprio per una gara contro il tempo come la penultima tappa di ieri al Tour.

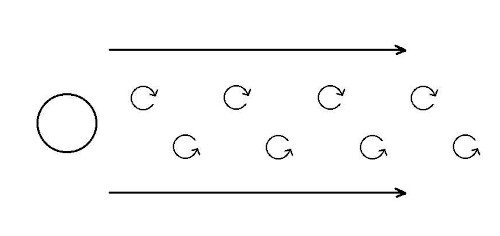
Nel prosieguo della discussione non mi soffermerò in aspetti comunque importanti come il moto di un fluido, la portata, il teorema di Bernoulli, ma su quello che succede quando un corpo si trova all'interno di un fluido. Il caso più semplice è sicuramente quello di una sfera immersa in un fluido: se il fluido è ideale, non si creano vortici e la sfera resta immobile. Questo è il così detto paradosso di d'Alembert. In generale si potrebbero avere comportamenti da fluido ideale in un fluido reale solo a velocità basse, almeno per quel che riguarda i vortici. La presenza dei vortici, comunque, modifica le pressioni lungo la superficie della sfera, che così viene trascinata dal mezzo.
In ogni caso un qualunque oggetto immerso in un fluido sperimenta la seguente resistenza: \[F_r = \frac{1}{2} cSRv^2\] dove \(S\) è la sezione, \(c\) un oggetto adimensionale che dipende dalla forma dell'oggetto immerso, \(v\) la velocità dell'oggetto (o se si preferisce la velocità relativa dell'oggetto rispetto al fluido).
La forza risulterà proporzionale alla velocità al quadrato nel caso di regime vorticoso, proporzionale a \(v\) e quindi coincidente con l'attrito viscoso, in caso di regime laminare, quando \(c\) è inversamente proporzionale alla velocità. Vediamo, ora, di chiarire i concetti di regime laminare e regime vorticoso.
Il primo è caratterizzato da basse velocità e dal fatto che la velocità del fluido a contatto con le pareti che lo contengono è praticamente nulla e cresce a strati man mano che ci si sposta verso il centro. Nel regime vorticoso, invece, le velocità sono più elevate e gli attriti interni hanno così la possibilità di creare dei vortici. In particolare esiste una velocità critica, che stabilisce il passaggio dal regime laminare a quello vorticoso, ed è stata trovata sperimentalmente da Osborne Reynolds.
Quando il parametro adimensionale detto numero di Reynolds \[R_e = \frac{\rho v R}{\eta}\] raggiunge il valore di 1200, la velocità critica per la transizione è data da: \[v_c = 1200 \frac{\eta}{\rho R}\] dove \(\rho\) è la densità del fluido, \(R\) il raggio del tubo in cui è contenuto, \(\eta\) la viscosità del fluido, che è dell'ordine di 10-2 per l'acqua, con piccole differenze al variare della temperatura, e dell'ordine di 10-7 per l'aria a 20° (più o meno a temperatura ambiente).
Come si vede, dunque, l'aria è un fluido estremamente meno viscoso rispetto all'acqua: questo spiega perché la depilazione è molto più vantaggiosa per i nuotatori che per ciclisti e sprinter: non è un caso che le tutine integrali non sono mai riuscite a sfondare nel mondo dell'atletica, dove i loro vantaggi sono estremamente bassi.
Tutte queste considerazioni, fatte spesso anche in modi più precisi e dettagliati, hanno come conseguenza il dover migliorare la posizione sulla bici, affiancando, ovviamente, le considerazioni opportune sulla potenza e quant'altro, alcune fatte anche negli altri articoli dedicati al Tour di quest'anno. Molti ciclisti, poi, sono entrati anche in galleria del vento, per studiare al meglio la posizione in ogni condizione di tempo: è questa una scelta, forse eccessiva per dei ciclisti, mutuata dal mondo della Formula 1, per restare nell'ambito dello sport, anche se in questo caso motoristico. La coincidenza dell'uscita di questo articolo con il Gran Premio di Germania di Formula 1, che vede Fernando Alonso e la Ferrari tornare in prima fila, mi ricorda che tra i concetti trascurati uno molto importante anche per la Formula 1 è sicuramente la portanza, viste le ali e le alette di cui sono normalmente riempite le automobili da corsa.
Sempre i corpi in movimento in un fluido possono, poi, subire l'effetto Magnus, che è importante soprattutto per gli oggetti sferici, come i palloni da calcio o le palline da tennis (ma anche quelle da golf).
A questo punto, in attesa che i motori si accendano in Germania e che le bici arrivino sui Campi Elisi in Francia, non mi resta che salutarvi e augurare una buona domenica a tutti!
P.S.: il lettore più attento avrà notato che non ho presentato equazioni differenziali, integrali e quant'altro. Questo per due motivi: innanzitutto non ho mai veramente approfondito questi aspetti matematici della fluidodinamica, e poi in questo caso larticolo sarebbe stato eccessivamente difficile. C'è poi un ulteriore terzo motivo: lasciatemi qualche argomento per poter parlare ancora di sport in altre occasioni!
Scalando il Tourmalet | Discesismi | Ologrammi da polso: placebo sportivi | Passo a due | In punta di sella



Nessun commento:
Posta un commento