
Particolarità della tappa di ieri, che da spunto per l'articolo di oggi, è stata la presenza della pioggia. L'acqua che cade e bagna l'asfalto e le strade, rende il percorso scivoloso e questo perché diminuisce il tanto poco amato attrito. Questo, infatti, è una forza non conservativa, eppure senza l'attrito ci verrebbe molto difficile camminare, figuriamoci andare in bicicletta. Fateci caso: se vi capita di andare su una lastra di ghiaccio, in quel caso si scivola proprio per la quasi completa assenza dell'attrito (non è un caso che il coefficiente d'attrito sull'asfalto bagnato è inferiore rispetto all'asfalto asciutto). E' in quel caso che si spiega lo scivolone sul ghiaccio: quel poco di attrito presente, infatti, consente al ghiaccio sotto le suole di sciogliersi e creare quindi le condizioni per la sua assenza, facendoci cadere a terra (i migliori con un doppio carpiato all'indietro).
Eppure, nonostante la piogga, i nostri due campioni si danno battaglia e Contador addirittura scatta, staccando per alcuni metri il suo avversario. Fermiamoci con questa immagine in mente, con la pedalata a metà, con la ruota ferma lungo l'asfalto bagnato. Come funziona quindi l'attrito, sul quale si era già discusso in altre occasioni (l'ultima esaminando le salite in bici), che permette ai ciclisti di andare in bici e più in generale a noi di camminare per le strade? In un certo senso l'attrito fa una sorta di passo a due con la gravità, proprio come i nostri due atleti sulla strada verso la cima conclusiva. Ma andiamo con ordine:
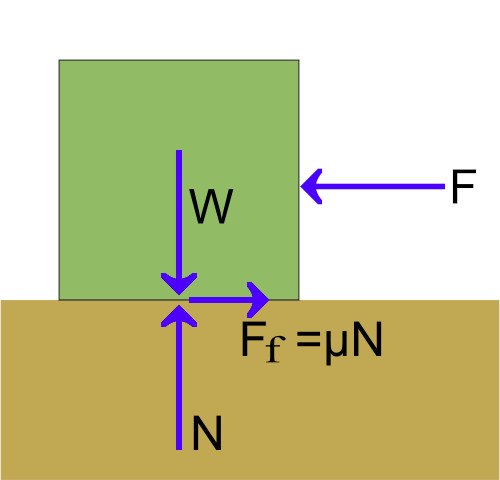
Quando poggiamo un oggetto sul tavolo o su una qualunque superficie, se vogliamo spostarlo, magari trascinandolo lungo il piano, la prima forza che dobbiamo vincere è la così detta forza di attrito statico: \[F_s = \mu_s N\] dove \(N\) è il modulo della componente perpendicolare della forza totale che agisce sul corpo (al massimo coincide con la forza di gravità, se spingiamo il nostro oggetto con una forza parallela al piano di appoggio), \(\mu_s\) il coefficiente di attrito statico. Non appena il corpo si sposta, l'attrito statico è sostituito dall'attrito dinamico: \[F_d = \mu_d N\] dove il coefficiente d'attrito dinamico \(\mu_d\) è più piccolo rispetto a \(\mu_s\).
Un modo (che ho utilizzato) per misurare l'attrito statico superficie è attaccare un dinamometro a un pesetto e leggere il valore \(F_D\) della forza nell'esatto istante in cui il corpo inizia a muoversi. In quel momento, in cui siamo praticamente prossimi all'equilibrio, possiamo affermare, senza commettere grossi errori, che la forza letta sul dinamometro coincide con l'attrito statico, e mantenendo il dinamometro parallelo al piano, il coefficiente di attrito statico sarà dato da: \[\mu_s = \frac{F_D}{P}\] dove \(P\) è la forza peso del corpo che stiamo cercando di spostare.
Se l'esperimento è ben fatto, si dovrebbe ottenere una misura abbastanza accurata del coefficiente di attrito, ma in ogni caso può essere interessante per capire le difficoltà da affrontare non solo nella progettazione, ma anche nell'esecuzione di una attività sperimentale.
L'attrito di cui abbiamo discusso fino a ora è però il così detto attrito radente, un attrito che, come si intuisce dalla parola, è tipico dello strisciare. Esistono almeno altri due tipi di attriti, uno viscoso, cui spero di dedicare una discussione a parte, e un altro detto volvente. Per introdurlo, però, torniamo alla ruota dei nostri ciclisti, quella che avevamo lasciato ferma lungo la salita del Tourmalet.
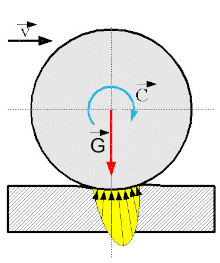
In questo caso la velocità del centro di massa è data da: \[\vec V_{CM} = - \vec \omega \wedge \vec r\] dove \(\omega\) è la velocità angolare, ovvero il numero di giri che per esempio la ruota della bicicletta fa nell'unità di tempo, mentre \(r\) è il raggio della ruota. Questo vuol dire che per migliorare la velocità si può o aumentare il raggio della ruota o aumentare il numero di giri al minuto. Ed è su quest'ultimo punto che gli atleti si allenano per migliorare le loro prestazioni sportive.
A questo punto, anticipando un attimo il discorso sulla cronometro, si può calcolare anche l'accelerazione di una ruota. Prendiamo il caso di una ruota ad alto profilo, una di quelle generalmente utilizzate per tali generi di gare. In questo caso, supponendo la ruota omogenea e quindi con un momento di inerzia pari a \[I = \frac{1}{2} M r^2\] allora l'accelerazione del centro di massa sarà data da \[a_{CM} = \frac{2}{3} \frac{rF + M}{mr}\] con una forza di attrito pari a \[F_a = \frac{2M - rF}{3r}\] dove \(M\) è il momento angolare della ruota, \(F\) la forza applicata al centro di massa della ruota, che poi coincide con il suo centro.
Nota importante: nel puro rotolamento l'attrito non compie lavoro, questo perché, come già spiegato in precedenza, vinto l'attrito, che è sempre statico in ogni momento del rotolamento, il punto di applicazione della forza si allontana immediatamente. Quindi niente spostamento, niente lavoro e così l'energia si conserva.
Eppure si osserva che anche una ruota che si muove rotolando e senza strisciare lungo un piano e senza l'intervento di forze esterne, dopo un certo tempo si ferma. Questo perché entra in gioco l'attrito volvente: attribuito alla deformazione del piano, dal punto di vista matematico può essere rappresentato dal seguente momento angolare volvente: \[M_v = hmg\] dove \(h\) è il coefficiente di attrito volvente. Per vincere questo momento, bisogna applicare alla ruota una forza di trazione uguale o superiore a \[F = \frac{hmg}{r}\] con \(r\) raggio della ruota.
Volendo confrontare i due tipi di attrito, quello dello strisciamento con quello del rotolamento, si può procedere calcolandone il rapporto: \[\frac{F_s}{F_v} = \frac{\mu_s}{h}r\] e considerando che il rapporto tra \(h\) coefficiente di attrito volvente e \(r\) raggio della bicicletta è dell'ordine di 10-5, è abbastanza evidente che far rotolare una ruota è molto più semplice e vantaggioso che farla strisciare.
Scalando il Tourmalet | Discesismi | Ologrammi da polso: placebo sportivi | Passo a due | In punta di sella

Nessun commento:
Posta un commento