Ritratti: Guglielmo Marconi

Nel 1909 Guglielmo Marconi, insieme con Ferdinand Braun, vinse il Premio Nobel per la Fisica. La motivazione fu identica per entrambi:

in recognition of their contributions to the development of wireless telegraphy⁽¹⁾

In pratica fu proprio l'invenzione della radio, quell'elettrodimestico che doveva essere soppiantato dall'arrivo del televisore, che portò Marconi alla vittoria dell'ambito premio a 35 anni.
Nato il 25 aprile del 1874, visse e studiò tra Inghilterra (la madre, Annie Jameson, era irlandese) e Italia. Qui la sua base fu Livorno dove, grazie agli stimoli del professore Vincenzo Rosa, che insegnava fisica presso il locale liceo, si interessò all'elettricità e all'elettromagnetismo, prendendo ben presto la strada delle applicazioni pratiche piuttosto che quella dell'approfondimento teorico, probabilmente preferita e consigliata da Augusto Righi, docente dell'Università di Bologna.
Per sua e nostra fortuna, il giovane Guglielmo decise di approfondire gli aspetti sperimentali, pratici e imprenditoriali dell'elettricità.

Discorso di Hildebrand ai Nobel del 1909

100 anni fa veniva assegnato a Guglielmo Marconi il Nobel per la Fisica per il suo lavoro nelle telecomunicazioni senza fili, in pratica per l'invenzione della radio. 100 anni fa, di questi tempi, Marconi, insieme agli altri vincitori del Nobel, andava a ritirare il Premio. Questa è dunque la "Settimana Nobel" durante la quale si festeggia il centenario del Premio Nobel a Marconi. Per iniziare vorrei proporvi il discorso di presentazione di Hans Hildebrand, archeologo, ex Rettore Generale del Museo Nazionale di Antichità e Presidente dell'Accademia Reale Svedese delle Scienze, il 10 dicembre del 1909:

---

Vostra Maestà, Vostre Altezze Reali, Signore e Signori,
La ricerca nel campo della fisica ci ha regalato molte sorprese; scoperte che in un primo tempo sembravano di mero interesse teorico hanno spesso portato a invenzioni di enorme valore per il progresso dell'umanità. E se questo si può dire per la fisica in generale, è ancor più vero per la ricerca in ambito elettrico.
Le scoperte e invenzioni per le quali quest'anno l'Accademia Reale delle Scienze ha deciso di assegnare il Premio Nobel per la Fisica hanno anch'esse origine in opere e studi di natura puramente teorica e, per quanto importanti e rivoluzionarie siano state nei loro settori, nessuno avrebbe mai potuto indovinare le applicazioni pratiche che ne sarebbero risultate in seguito.

La dialettica tra scienza e fede

Ho apportato poche modifiche rispetto al post originale (archive.org) di cui quelle più importanti sulla qualità delle foto scattate all'epoca.

---

A questo, di fatto, si è ridotto l'incontro di ieri alla Feltrinelli per la presentazione di Hai vinto, Galileo di Piergiorgio Odifreddi, che era passato dalla Feltrinelli in primavera, accompanato da Dario Fo, per presentare In principio era Darwin.
Questa volta, in occasione del 150.nario della pubblicazione de L'origine della specie, si fa accompagnare da Vito Mancuso, amico del logico e soprattutto rappresentante dell'altra campana, quella dei credenti. In effetti Odifreddi e Mancuso fanno due lunghi interventi ciascuno, calamitando l'attenzione del pubblico per un paio d'ore, ma sottraendo il tempo per le domande conclusive e sfidando uno le ragioni dell'altro quasi con l'intenzione di voler risolvere l'annosa disputa fede-scienza.

Il ciclo dell'acqua

Per ciclo dell'acqua si intende il processo che genera, in un ciclo quasi chiuso, le nuvole a partire dall'acqua planetaria, le quali a loro volta rigenerano le acque terrestri attraverso le piogge.
Partendo dalle acque superficiali, il ciclo inizia con l'evaporazione, da cui il vapore acqueo che costituisce le nuvole che solcano, a varie altezze, il cielo sopra le nostre teste. Una piccola percentuale, l'1% circa, proviene dalla trasporazione delle piante.
Una volta nei cieli, l'acqua terrestre diventata nuvole, ricade sulla terra sotto forma di pioggia, ma anche grandine e neve (come effetto collaterale, le precipitazioni riportano sulla superficie parte degli agenti inquinanti catturati nel processo di formazione delle nuovole, ma questa è un'altra storia).
Parte delle precipitazioni vengono poi catturate dalle piante, mentre una parte si infiltra nel suolo per alimentare le acque sotterranee, che si muovono molto più lentamente di quelle superficiali. Queste ultime, invece, costituite da fiumi, torrenti, laghi, alimentano mari e oceani e forniscono buona parte dell'acqua potabile che consumiamo ogni giorno, imbottigliata per quattro soldi dalle multinazionali e poi rivenduta dieci volte e più rispetto al prezzo di affitto.

Singolarità nuda

Illustrazione di Gavin Potenza

Nella maggior parte dei casi sono le news scientifiche a propormi articoli e combinazioni, o magari qualche articolo pubblicato su qualche blog che seguo, ma a volte è semplicemente il caso che mi fa trovare le idee per gli articoli che vi propongo, come ad esempio per l'equazione di Dirac e quella di Klein-Gordon, quando una semplice segnalazione via e-mail di un seminario divulgativo a Londra è esplosa in un piccolo racconto sulle due equazioni.
Anche l'articolo sulla singolarità nuda di oggi fa parte della categoria caso, e in particolare sono due le fonti/pensieri che lo hanno ispirato.
Da una parte la scoperta del sito The Naked Army!, realizzato da una studentessa (o ricercatrice?) di lettere, dunque una persona seria secondo i canoni comuni, che mi ha fatto nascere il pensiero: ecco che per fare traffico biosgna mettere in mostra il nudo e il corpo femminile e non; come posso fare la stessa cosa?
La risposta è stata immediata: singolarità nuda. Però lo spunto definitivo arriva con l'immagine di presentazione dell'articolo: una Terra che sta cadendo all'interno di una singolarità gravitazionale (da Synaptic Simuli).

The life and times of Paul Dirac

Una teoria fisica deve possedere belezza matematica.

A dirlo è Paul Dirac, uno dei più grandi fisici teorici di ogni tempo. La così detta equazione di Dirac, che insieme con quella di Klein-Gordon descrive il mondo quantistico-relativistico, è uno dei suoi massimi successi e l'interpretazione dei suoi risultati una delle sue più grandi soddisfazioni nel momento in cui questa è stata confermata dalle osservazioni.
Per un fisico la bellezza di un'equazione risiede spesso nella sua sinteticità e nella quantità di informazione fisica che è in grado di sintetizzare e quindi la grande varietà di sistemi che può rappresentare. Ad esempio l'equazione di Schrodinger, nella sua forma più sintetica, è in grado di descrivere sistemi tra i più disparati, e solo scendendo nel dettaglio di ciascun sistema, i fisici sono in grado di descrivere con soluzioni più o meno complicate il sistema stesso. \[i \frac{\partial \psi}{\partial t} = H \psi\] Qualcosa del genere fanno le equazioni ideate da Klein-Gordon e da Dirac, ma per il mondo relativistico: le particelle di cui è costituita la materia, infatti, sono in grado di viaggiare anche a velocità prossime a quelle della luce e in quel caso l'equazione di Schrodinger non è più sufficiente per descrivere la loro dinamica.
Da questa esigenza, dunque, di descrivere il mondo relativistico dal punto di vista quantistico, nasce l'equazione di Klein-Gordon,

Il libro dei rompicapi di Alice

---

Titolo: Il libro dei rompicapi di Alice
Autore: Lewis Carroll, John Fisher (a cura di)
Edizione: Costa & Nolan

Da un'annotazione sul suo diario datata marzo 1875 si sa che il reverendo Charles Lutwidge Dodgson, matematico e divulgatore, meglio noto come Lewis Carroll, aveva in animo di raccogliere buona parte dei suoi enigmi e giochi matematici pubblicati su riviste, libri e romanzi, dal titolo Il libro dei rompicapi di Alice. A distanza di poco più di un secolo è John Fisher, studioso di letteratura, a dare corpo al sogno dell'autore di Alice nel Paese delle Meraviglie, sempre con lo stesso titolo ideato a suo tempo da Carroll. Oggi il libro torna nelle librerie italiane grazie alla Castor & Nolan, regalandoci un percorso nella matematica e nell'illusione che si nasconde dietro Alice e le altre opere di Carroll, di cui abbiamo già avuto un primo assaggio.
Fisher organizza il libro in maniera semplice ma ben argomentata e approfondita, strutturandolo in piccoli capitoli dedicati ognuno a un gioco, matematico, logico o illusionistico (Carroll era, infatti, anche un appassionato di giochi di prestigio e un illusionista dilettante), ispirato alle opere dedicate ad Alice, ma anche alle altre sue opere, come La caccia allo Snark, o il divulgatico Logica Simbolica, o dagli articoli usciti sulle più disparate riviste, come ad esempio Vanity Fair o la prestigiosa Nature.
Nel corso del libro si passa da giochi matematici, a giochi logici, alla descrizione di divertenti giochi illusionistici, ma si scopre anche la propensione di Carroll a ridefinire le regole dei giochi più disparati, come il prestigioso polo, che ha il suo spazio nel Paese delle Meraviglie, o l'ideazione ex novo di un gioco il cui intento era quello di rendere più semplice l'apprendimento della logica per i bambini.
In quest'ultimo campo, però, si registrano degli insuccessi da parte di Carroll, che riesce ad attrarre l'attenzione solo degli addetti ai lavori, i logici (e personalmente non stento a crederlo), ma proseguendo nell'esame del libro, è anche interessante il capitoletto dedicato agli origami, in cui si parte dalla striscia, o nastro di Möbius, per poi passare a descrivere le operazioni per realizzare alcune figure particolari. Un piccolo spazio se lo ritagliano anche gli scacchi, uno dei giochi preferiti da Carroll, tanto che era solito con alcuni amici e allievi, giocare partite mentalmente.
In definitiva un libro ricco di giochi e aneddoti, stimolante e divertente, che non può mancare di appassionare l'enigmista e il matematico che è in ognuno di noi.

I rompicapi di Alice: Il numero magico

Ed eccoci con una nuova serie, che spero non sostituisca la Matematica in gioco (l'ultimo appuntamento a metà luglio con i reticoli euleriani), ma questo solo il tempo potrà dircelo.
L'accenno non è poi così casuale, visto che il rompicapo di oggi, è legato al party a base di te di Alice, Cappellaio Matto e Lepre Marzolina. In quella festa, infatti, c'è anche un accenno al tempo e agli orologi, e qui, da buon wikipediano, divago: riguardo gli orologi, infatti, vi consiglio di leggere il divertente articolo dei Rudi Mathematici sul 4 negli orologi (nella mia recente visita al Museo Leonardo ho effettivamente verificato l'anomalia rilevata dai nostri prodi matematici: a presto con una apposita galleria fotografica, che anche in questo caso sarà il tempo a dirci se e quando verrà!).
Comunque, divagazioni a parte, un po' ispirato dall'ultimo Carnevale un po' dalla lettura de Il libro dei rompicapi di Alice, curato da John Fisher su carte, appunti e articoli di Lewis Carroll, eccovi una nuova capatina nel mondo di Alice e compagni, questa volta con un appuntamento che, per quanto saltuario e mai preciso, spero possa allietarvi di tanto in tanto, ogni volta che emerge improvviso dalle nebbie un po' come la fantomatica e leggendaria isola di Brigaboom.

Black Holes and Revelations

Cygnus X1

E' stato recentemente scoperto un buco nero supermassiccio: Fabio De Sicot di Caccia al fotone sul suo blog associa con la nota canzone dei Muse la news scientifica. Questo mi ha ispirato il titolo di questo articolo, che è anche il titolo del penumltimo disco del grandissimo gruppo britannico: vi racconto in questo caso della realizzazione in laboratorio di un simil buco nero (e non un buco nero fai da te o anche tascabile come qualcun altro ha proposto).
Di buchi neri in laboratorio molti giornali e televisioni si sono riempiti la bocca all'alba della prima accensione dell'LHC, inondando l'etere dei timori sulla distruzione della Terra ad opera di un mini buco nero che avrebbe potuto essere creato all'interno dell'anello dell'acceleratore di particelle.
D'altra parte ad agosto su Physical Reviews Letters, Nation, Blencowe, Rimberg e Buks, hanno proposto l'uso di un superconduttore per investigare una radiazione analoga a quella di Hwaking.
Nell'articolo i ricercatori mostrano che un campo magnetico pulsante che circonda un reticolo di dispositivi di interferenza superconduttivi, non solo riproduce fisica analoga a quella di una radiazione di un buco nero, ma anche le proprietà quanto-meccaniche in sistemi ben noti che possono essere controllati direttamente in laboratorio.
E recentemente è stato costruito un nuovo dispositivo che imita gli effetti di un buco nero, senza i suoi effetti collaterali.

Ritratti: Ada Yonath

Finora l'unica biografia femminile nei Ritratti è stata quella di Rita Levi Montalcini, vincitrice del Premio Nobel per la medicina nel 1986. L'occasione per parlare di un'altra donna scienziata me la da l'assegnazione del Nobel per la Chimica 2009, vinto tra gli altri da Ada Yonath.
Certo mi sarebbe venuto più facile scrivere di Venkatraman Ramakrishnan, il fisico che ha condiviso il premio insieme alla scienziata israeliana, però ho pensato di proporre una figura femminile, che spesso manca negli ambienti scientifici e anche nelle statistiche del Premio per la Chimica.
Nata il 22 giugno 1939 a Gerusalemme è nota soprattutto per i suoi pionieristici studi sul ribosoma. Si guadagna il bachelor in chimica nel 1962 e il master in biochimica nel 1964 (gli equivalenti delle nostre laurea breve e laurea magistrale). Successivamente lavora presso la Carnegie Mellon (1969) e quindi al MIT (1970). 10 anni più tardi, nel 1979, la ritroviamo a Berlino, al Max Planck Institute for Molecular Genetics, a dirigere ricerche insieme a Heinz-Guenter Wittmann fino al 1984. La ritroviamo, quindi, dopo un anno sabbatico, passato presso l'Università di Chicago, al Max Planck Institute di Amburgo nel 1986 dove porterà avanti la sua attività di ricerca dino al 2004 in parallelo con quella presso il Weizmann Institue, dove lavora tutt'ora.

Carnevale della Matematica #18

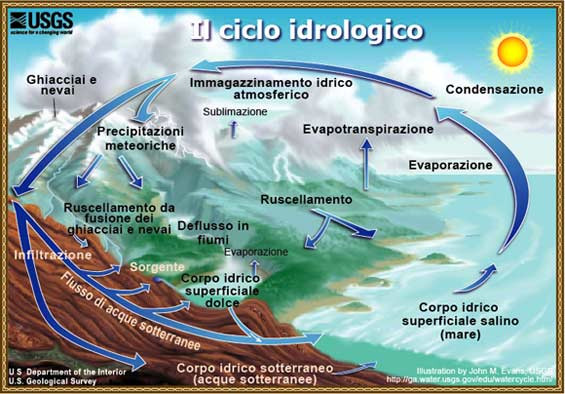
Iniziamo con un bell'almanacco storico: correva l'anno 18 quando Artaxias III succede a Vonone I sul trono dell'Armenia, mentre il 16 settembre nasce Drusilla, sorella dell'imperatore Caligola e nota divinità con il nome di Diva Giulia. Ci lasciano, invece, Erode Archelao e Publio Ovidio Nasone, valente poeta.
Le cronache, poi, ci dicono che Tiberio e Germanico vengono eletti consoli della Repubblica. Nello stesso anno, invece, la Augusta, terza legione Romana fondata da Augusto una sessantina di anni prima, viene sconfitta in un'imboscata in Africa (eh! non ci sono più le legioni di uyna volta!). Da una sconfitta, però, si passa ad una vittoria, quella di Arminio, condottiero tedesco della Repubblica, sui Marcomanni.
Finito l'almanacco storico sull'anno 18, passiamo all'ambito scientifico, a noi carnevalisti sempre gradito: in questo caso doveroso ricordare che 18 anni fa moriva Rodolfo Benevento, matematico italiano, che ha anche insegnato presso l'Università della Calabria, e quindi caro a questo umile blogger.
Il 6 agosto, sempre di 18 anni fa, nasceva invece il world wide web, creato da Tim Berners-Lee, che metteva online la prima pagina html, e da Robert Cailliau, entrambi ricercatori del CERN. Inoltre il 1° ottobre, sempre di 18 anni fa qualora ve lo foste dimenticato, veniva trasmessa la prima puntata dei Simpson.
A questo punto, prima che il Cappellaio Matto dia di matto per l'assenza di musica in questa festa di non-compleanno (chi compie gli anni oggi, è meglio che stia zitto se non vuole essere mandato via!), passiamo alle associazioni musicali, per la prima volta proposte ai carnevalisti dal sempre puntuale .mau.. Parto con il 18.mo disco dei Kiss, Psycho Circus (a mio parere il migliore della serie), semplicemente perché è loro l'album più vicino ai nostri carnevaleschi consessi, quel Carnival of Souls: The final sessions che però è il 17.mo della mitica band hard rock. Restando in tema di album, ricordiamo che quello del 2002 di Moby si intitolava, indovinate un po', 18! Non dimentichiamo poi Hanger 18 dei Megadeth, singolo estratto dall'album Rust in piece del 1990 mentre, andando un po' più indietro fino al 1971 abbiamo I'm eighteen del grandissimo Alice Cooper. Il singolo, estratto da Love it to death, è anche il primo dell'artista ad essere entrato nella top ten.
Mentre i primi invitati al party si stanno avvicinando, eccovi altre associazioni, in questo caso decisamente folkloristiche: 18, infatti, è il numero delle scimmie presenti nei templi shaolin, ma è anche il numero dei livelli dell'inferno cinese.
Non di solo folklore si sopravvive, ma anche di curiosità, che poi sono quelle che mi ha passato sotto banco la Lepre Mazolina: a quanto sembra il comune di Parma ha messo all'asta, un mesetto fa, ben 18 pecore, mentre alla fine della crono a squadre del Tour de France di quest'anno il rientrante Lance Armstrong (nessuna parentela con il nostro Armstrong) ha perso la maglia gialla per soli 18 centesimi!
In ogni caso, prima che il Cappellaio si arrabbi, vorrei ricordarvi che il nostro carnevale, a differenza di quello che cantava Alice Cooper, ha appena un anno e mezzo di vita. Calmato così il nostro anfitrione sul fatto che non è il nostro compleanno, non mi resta che invitare la Regina di Cuori a calmarsi cambiando sport per il più salutare golf, che, guarda un po', ha proprio 18 buche!
E ora diamo inizio alla festa:

---

Nobel 2009: un riepilogo

Nella prima parte dell'articolo, dopo un riepilogo con alcune considerazioni sparse sui premi di quest'anno, esamino le percentuali assolute dei Nobel al femminile. Nella seconda parte mi concentro su alcune considerazioni generali e su uno studio dei premi al femminile a partire dal 1990 a oggi, coprendo così un arco di tempo di 20 anni.

La marcia delle donne

Innanzitutto facciamo un riassunto dei Nobel di quest'anno:

• Medicina a Elizabeth Blackburn, Carol Greider e Jack Szostak.
• Fisica a Charles Kuen Kao, che vince metà del premio, mentre l'altra metà va a Willard Boyle e George Smith: questo è il Nobel più marconiano, nell'anno dell'anniversario dei 100 anni del Nobel all'ingegnere e fisico italiano, andato a tre ingegneri che hanno dedicato il loro lavoro alle telecomunicazioni.
• Chimica a Venkatraman Ramakrishnan, Thomas Steitz e Ada Yonath: in questo caso abbiamo l'unico fisico che ha vinto il Nobel quest'anno, Ramakrishnan, che ha utilizzato proprio metodi presi dalla fisica delle particelle per ricostruire la struttura del ribosoma.
• Letteratura a Herta Müller: per molti lettori, seriali e non, è una autrice praticamente sconosciuta, come ci ricorda anche Sara Faraoni di Camaleonte, che diventa anche un modo per discutere sulla diffusione della letteratura in Italia da parte di Alessandro Ghebreigziabiher.
• Pace a Barack Obama: un premio al futuro piuttosto che al passato, un voto sulla fiducia che oscilla tra i proclami di economia verde e gli accordi nucleari
• Economia a Elinor Ostrom e Oliver Williamson, due motivazioni diverse ma un premio epocale visto che per la prima volta va a una donna, come ci fa notare anche Gravità Zero.

Nobel 2009: Economia

E oggi si è conclusa la prima parte della cerimonia dei Nobel, con l'assegnazione del Nobel per l'Economia. Quest'anno, come raramente accade per questo premio, l'assegnazione è stata multipla, così come le motivazioni.
Decisamente molto a sorpresa, quest'anno è stato assegnato il primo Nobel femminile per l'Economia a Elinor Ostrom dell'Università dell'Indiana a Bloomington con la seguente motivazione:

for her analysis of economic governance, especially the commons

La sua attività si è concetrata soprattutto sullo studio delle risorse comuni: in effetti può essere considerata una sostenitrice di un'economia sostenibile, almeno leggendo la lista delle sue pubblicazioni (in particolare l'articolo del 2009 uscito su Science 325(5939)). Si occupa anche di scienze politiche (disciplina nella quale si è laureata e ha preso il PhD) e amministrazione pubblica, come forse intuibile dalla motivazione del premio.
Il secondo premio è andato a Oliver Williamson di Berkeley con la seguente motivazione:

for his analysis of economic governance, especially the boundaries of the firm

La carriera di Williamson, almeno stando alle pubblicazioni scientifiche, si sviluppa tutta intorno allo studio del governo economico, quindi in linea perfetta con la motivazione del premio. Si occupa anche di contratti, finanza corporativa, costi di transazione: in quest'ultimo campo ha sviluppato una serie di idee riguardo le transazioni incomplete e il rapporto azienda-fornitore. Williamson è da considerarsi, per studi e carriera, un economista puro.
Si chiude, scrivevo sopra, la serie di annunci Nobel per il 2009. L'appuntamento è per domani con alcune considerazioni finali.

Nobel 2009: Pace

Il Nobel più atteso, quello per la Pace, viene quest'anno assegnato al Presidente degli Stati Uniti d'America Barack Obama con la seguente motivazione:

for his extraordinary efforts to strengthen international diplomacy and cooperation between peoples

L'attuale amministrazione statunitense, dunque, è sempre più caratterizzata da un alto tasso di Premi Nobel (ricordiamo il Nobel per la Fisica Steven Chu, che ha recentemente siglato un accordo con l'Italia sullo sviluppo dell'energia nucleare).
Personalmente lo prendo come un premio alla fiducia, visto che quello che resta da fare è ancora più di quello che è stato fatto, anche se sicuramente è stata premiata una persona, un uomo che ha lavorato per la pace e non solo in maniera più incisiva ed efficace di molti suoi recenti predecessori come laureates del Premio.
E adesso un fine settimana di pausa prima della chiusura con il Nobel per l'Economia.

Nobel 2009: Letteratura

E continuiamo ad occuparci di Nobel, con quello per la Letteratura assegnato da ormai pochi minuti a Herta Müller, scrittrice tedesca di origine rumena. Questa la motivazione del premio:

who, with the concentration of poetry and the frankness of prose, depicts the landscape of the dispossessed

Il premio alla Müller ha anche, come spesso accade, un sapore che va al di là dei meriti letterari del premiato: la scrittrice, infatti, trasferitasi in Germania al seguito del marito Richard Wagner (non è lo stesso delle valchirie, per fortuna!), non ha rinunciato all'impegno politico sia contro il regime di Ceausescu, sia per criticare, laddove necessario, l'attuale politica rumena (come in questa occasione).
Oltre all'attività di scrittrice, la Müller è anche poetessa e traduttrice. E a questo punto non mi resta che dare appuntamento al Nobel più atteso, quello per la Pace, e non dimenticatevi il concorso lanciato da Gravita Zero: potrete finire per una volta come firma su uno dei migliori corporate blog divulgativi che contiamo in Italia. E Science Backstage? Ne parleremo la settimana prossima dopo l'assegnazione dell'ultimo Nobel e l'inevitabile post riassuntivo.

Nobel 2009: Chimica

Ed eccoci all'appuntamento con l'ultimo Nobel scientifico, quello per la Chimica (sfido chiunque a dire che il Nobel per l'Economia, l'ultimo a venire assegnato, ha un che di scientifico!). Quest'anno il Nobel è andato alla terna Venkatraman Ramakrishnan degli MRC Laboratory of Molecular Biology (e che da un gusto un po' più fisico al premio per la chimica, come vedremo più sotto), Thomas Steitz di Yale e Ada Yonath del Weizmann Institute of Science, con la seguente motivazione:

for studies of the structure and function of the ribosome

I robosomi, presenti all'interno della cellula, sono costituiti dal così detto RNA ribosomiale, o r-RNA, e da proteine: essi sintetizzano le proteine a partire dall'm-RNA, o RNA messaggero e furono osservati per la prima volta al microscopio elettronico nel 1953 da George Palade, vincitore del Nobel nel 1974 insieme ad Albert Claude e Christian de Duve per la scoperta del vacuolo.
Tornando ai premiati di quest'anno, c'è da notare che il gruppo di Ramakrishnan, il più giovane dei tre, ha recentemente determinato la struttura atomica completa del ribosoma: si parla di articoli che partono dai primi anni Ottanta del XX secolo per farsi via via più fitti con i questi ultimi tre-quattro anni. Un Nobel abbastanza giovane con una attività sul ribosoma anche piuttosto recente. Da buon fisico, poi, non mi resta che far notare come Ramakrishnan, insieme con Tanaka, conta una pubblicazione nel 1977 su Physical Review B di un articolo sulle transizioni di fase e sulla funzione di Green, Green's function theory of the ferroelectric phase transition in potassium dihydrogen phosphate, argomento che vede i fisici come sempre all'avanguardia.

Nobel 2009: Fisica

Sono contentissimo per l'assegnazione del Nobel per la fisica di quest'anno. L'annuncio, di poche decine di minuti fa, in diretta web mondiale, sembra un modo dell'Accademia di festeggiare i 100 anni del Nobel a Marconi. Metà del premio, infatti, è andata a Charles Kuen Kao con la seguente motivazione:

for groundbreaking achievements concerning the transmission of light in fibers for optical communication

Kao, ingegnere, lavora presso gli Standard Telecommunication Laboratories di Harlow e con l'Università cinese di Hong Kong.
L'altra metà del premio, invece, se la dividono Willard Boyle e George Smith, entrambi dei Bell Laboratories di Murraj Hill negli Stati Uniti, con la seguente motivazione:

for the invention of an imaging semiconductor circuit – the CCD sensor

Anche in questo caso il premio sembra sia stato assegnato a fagiolo: l'invenzione del charge coupled device risale giusto a 40 anni fa, al 1969. Il sistema ideato da Boyle, che è intervenuto telefonicamente alla conferenza stampa, e Smith è un circuito integrato costituito da semiconduttori in grado di accumulare una quantità di carica elettrica proporzionalmente con l'intensità del campo elettromagnetico che li colpisce. L'accoppiamento tra i semiconduttori è tale per cui l'impulso elettrico si trasferisca da vicno a vicino: in pratica un'interazione a primi vicini, o qualcosa del genere.
Un dispositivo del genere è utilizzato soprattutto nei sistemi che devono riprodurre immagini più o meno complesse: lo ritroviamo infatti in sistemi come fotocamere, macchine fotografiche, fax, scanner, ma ha anche applicazioni in astronomia.
I tre vincitori, dunque, sono in un certo senso legati uno all'altro per aver contribuito a migliorare la trasmissione e la qualità delle informazioni nella nostra era moderna.
A questo punto, sperando che l'anno prossimo il Nobel per la fisica vada a un teorico, non mi resta che rimandare a nuovi aggiornamenti per i prossimi Nobel.

Nobel 2009: Medicina/Fisiologia

Dopo l'assegnazione degli Ig, inizia quella dei Nobel.
Da poche ore, infatti, sul sito del premio è stato pubblicato l'annuncio dell'assegnazione del Nobel per la Medicina/Fisiologia per il 2009 a Elizabeth Blackburn dell'Università della California, Carol Greider della John Hopkins e Jack Szostak di Harvard (e altri istituti). Il premio è stato assegnato con la seguente motivazione:

for the discovery of how chromosomes are protected by telomeres and the enzyme telomerase

ovvero per i loro studi sulla telomerasi, un enzima che protegge i cromosomi.
Come fa notare Claudio Pasqua su Gravità Zero

E' la prima volta che l'annuncio viene dato attraverso un sistema di video-streaming direttamente dal sito web nobelprize.org, dunque in diretta-live mondiale.

Purtroppo il live me lo sono perso, ma l'annuncio non rinuncio a comunicarvelo.
Ci aggiorniamo con i prossimi Nobel.

Ig Nobel 2009

Il 3 ottobre si sono tenute le Ig Nobel Informal Lectures, delle lezioni informali tenute dai vincitori dei premi. Gli Ig Nobel sono uno dei premi più divertenti ma anche tra i più ambiti, dopo i Nobel of course, nel mondo scientifico, e il motivo è semplice: per ricerca improbabile si intende una ricerca che fa ridere ma anche pensare. L'obiettivo dell'associazione, Improbable Research, è quindi quello di utilizzare la scienza per divertire e stimolare la curiosità scientifica, la ricerca verso nuove domande, divulgare la passione per la scienza. Tra l'altro molte ricerche imporbabili vengono anche pubblicate sulla rivista Annals of Improbable Research.
I premi migliori? Quelli per sanità pubblica, letteratura, fisica, biologia, chimica.
Veniamo, però, alla lista dei vincitori, che riprendo da Gravità Zero:

La sfera di Matem@ticamente: Raccolta la sfida

Annarita Ruberto lancia una nuova sfida matematica, che io da buon fisico questa volta raccolgo. Come potrete immaginare dall'immagine a corredo, la sfida e la mia soluzione sono legate al principio di Archimede. Andiamo, però, con ordine:
Se immergo un corpo in un fluido, esso subirà una spinta dal basso verso l'alto pari al peso del fluido spostato. In formule \[S = P_f = \rho_f V_s g\] dove $\rho_f$ è la densità del fluido, $V_s$ il volume spostato, $g$ l'accelerazione di gravità.
La forza totale che agisce su un corpo immerso sarà quindi: \[F_{tot} = \rho_c V_s g - \rho_f V_s g\] dove $\rho_c$ è la densità del corpo.
Con questi ingredienti, esaminiamo il problema proposto da Annarita: la forza che agisce sulla sfera immersa nel cilindro sarà \[F_{tot} = \rho_S V_S g - \rho_a V_S g\] dove $\rho_S$ è la densità della sfera, $\rho_a$ quella dell'acqua, $V_S$ il volume della sfera.
Il peso del cilindro (inteso come la forza peso del cilindro) sarà invece dato da \[P_C = T + \rho_a V_C g\] dove $T$ è la tara, $V_C$ il volume del cilindro.
Una volta immersa la sfera nel cilindro, il suo peso aumenta di 20 Kg (ricordo che la sfera pesa invece il doppio, 40 Kg). Possiamo allora scrivere la seguente equazione: \[P_C - P_a + F_{tot} = P_C + 20 \, kg \cdot g\] dove $P_a$ è il peso dell'acqua espulsa dal cilindro dopo aver completato l'immersione della sfera. L'equazione comunque rappresenta questa situazione: a sinistra vengono inseriti gli ingredienti, ovvero il peso del cilindro meno quello dell'acqua espulsa più la forza che agisce sulla sfera⁽¹⁾; a destra il peso del cilindro più quello corrispondente ai 20 Kg in più.
Prima di eseguire i calcoli analitici, valutiamo il peso dell'acqua espulsa, che è identico a quello dell'acqua spostata⁽²⁾: \[P_a = \rho_a V_S g\] Considerando che 20 Kg = 40 Kg/2, ovvero 20 Kg = $mS/2$, l'equazione risolutiva diventa: \[\left ( \rho_S - 2 \rho_a \right ) V_S = \frac{1}{2} m_S\] da cui si ricava facilmente che \[\rho_S = 4 \rho_a\] mentre il volume del cilindro è dato dalla relazione \[V_C = \frac{3}{2} \frac{m_S}{\rho_S}\] A questo punto bisogna solo mettere nelle equazioni i dati del problema, ottenendo le risposte richieste da Annarita.
Ovviamente se dovessero esserci degli errori nel ragionamento o nello svolgimento, siete invitati a segnalarli nei commenti.

---

(1) Dobbiamo innanzitutto considerare che l'immissione della sfera ha espulso una certa quantità d'acqua, e quindi questo peso va sottratto, e poi a questo dobbiamo aggiungere il peso immerso della sfera, differente rispetto al peso effettivo a causa della spinta di Archimede.
(2) Ciò viene assicurato dal fatto che l'immersione della sfera è avvenuta lentamente.

Il problema del trasporto

Il problema del trasporto, così come formulato da Gaspard Monge nel 1781, si interroga su cosa succede quando si sposta una massa da un punto a un altro dello spazio. In un problema del genere bisogna tener conto della densità di massa, dei sottospazi in cui si trovano i due punti, $x$, $y$, e gioca un ruolo importante la così detta funzione dei costi, che in uno spazio euclideo viene definita con dalla norma usuale. Problemi di questo genere e la matematica sviluppata per risolverli, trovano svariate applicazioni: economia, analisi funzionale, probabilità e statistica, meteorologia e varie altre. Interessante, poi, come si potrebbe studiare in quest'ottica del problema del trasporto la riflessione su una superficie parabolica come un radar.
Un problema del genere, quindi, mostra una matematica più o meno complessa, ingredienti comunque semplici, una base fondamentalmente fisica, come d'altra parte alcune delle sue applicazioni, diventando così un argomento decisamente pluri-disciplinare.
E' con l'esame di questo problema che Neil Trudinger⁽¹⁾, professore dell'Australian National University ha deliziato la platea intervenuta ad assistere a Optimal transportation in the 21st century, ultimo seminario delle Lezioni Leonardesche, edizione 2009 (pdf). Al di là dei problemi del microfono (uno di quelli che si agganciano all'attaccatura della camicia, con l'acustica influenzata dai movimenti della persona che lo indossa), Trudinger sintetizza l'argomento con una interessante introduzione storica per poi passare alle diapositive più specifiche con definizioni matematiche ed equazioni. Interessante, negli strumenti utilizzati, anche l'uso dei tensori, ovvero di una matematica utilizzata nella relatività generale. In sintesi un argomento che effettivamente avvicina matematica e fisica, soprattutto considerando l'esempio del radar proposto durante il seminario.

The Chicken Equation

La gallina non è un animale intelligente. Lo si capisce da come guarda la gente.

Così cantavano Cochi e Renato alcuni decenni fa. Forse ha pensato la stessa cosa Doug Zongker quando ha presentato il divertentissimo seminario Chicken Chicken Chicken al PoCSci 2002. Il video è divertente, assolutamente esilarante, soprattutto quando arrivano le domande dal pubblico. L'articolo, poi, è un pezzo di scienza irripetibile. Mi ha colpito, da buon teorico, soprattutto l'equazione presente, la& Chicken equation del titolo. Eccovela: \[C(K) = \sum_{i=1}^n \Delta^2 (K_i) = \sum_{i=1}^n \left |E_i - K(H_i) \right |^2\] Ho provato a dare un'interpretazione dei simboli dell'equazione e questo è il risultato:
La funzione $C(K)$ è la misura della gallinità di un allevamento di galline, dove $\Delta (K_i)$ indica la densità di probabilità che la gallina $K_i$ sia una vera gallina, quindi si somma su tutti gli individui dell'allevamento $K$. La stessa quantità può essere espressa come il quadrato della differenza tra l'osservabile $E_i$, che indica il grado di intelligenza dell'individuo $i$-simo e $K(H_i)$, che indica la gallinità dell'individuo $i$-simo, questa volta rappresentato dal termine $H_i$ in quanto la gallina viene vista come componente dello spazio di Hilbert di tutte le galline dell'allevamento $K$: in quest'ultimo caso il primo termine della differenza è sperimentale, mentre il secondo è teorico.
Buon divertimento con il video. Maggiori dettagli su Gavità Zero.

Ritratti: Bernhard Riemann

Bernard Riemann

Forse è un po' eccessivo ridurre Riemann alla sua famosa Ipotesi, considerando che uno dei suoi risultati più importanti è la teoria degli integrali (che guarda un po' rientrano ad un certo punto nella trattazione dell'Ipotesi), però il suo nome resta comunque legato a quell'unico problema del secolo indicato da David Hilbert nel 1900 tra i suoi famosi 23 problemi e ancora non risolto.
Georg Friedrich Bernhard Riemann nacque il 17 settembre 1826 a Breselenz, in Germania. Secondogenito della coppia Friedrich Bernhard Riemann, pastore luterano, e Charlotte Ebell, come i fratelli dovette districarsi attraverso una vita breve e difficile: considerando che erano in 6 (4 femmine e 2 maschi), si può facilmente immaginare quanto difficile fosse per il padre portare del sostentamento alla famiglia. Dei 6 figli Riemann, solo la maggiore, Ida, ebbe una vita abbastanza lunga per i canoni dell'epoca. Insieme alla famiglia, Riemann visse a Quickborn buona parte dei suoi migliori anni, sentendo in quel posto tutto il calore della famiglia e dei suoi affetti. Per poter coltivare, però, gli studi, il giovane fu costretto a trasferirsi ad Hannover, ambiente dove, anche a causa della sua timidezza, non si trovò mai bene. Il passo successivo che lo avvicinò alla matematica e a Gottinga fu Luneburg, dove conobbe un insegnante di ebraico grazie al quale riuscì ad andare nell'Università di Gauss per studiare, all'inizio, teologia e seguire così le orme del padre: era il 1846.

QED

---

Titolo: QED - La strana teoria
della luce e della materia
Autore: Richard Feynman
Edizione: Adelphi

Uno dei problemi che più ha alimentato la discussione tra i fisici è stata la natura particellare o forse ondulatoria della luce. E una delle scoperte più sconcertanti è stata invece il comportamento ondulatorio delle particelle. Andiamo, però, con ordine: per molti secoli a partire da Isaac Newton, che però pensava alla luce come composta da particelle, si descrissero i fenomeni ottici come ondulatori. La spiegazione era sufficientemente coerente con le osservazioni sperimentali, ma la sempre maggiore raffinatezza con cui questi iniziarono ad essere condotti mise in dubbio l'assunto. In certe condizioni, infatti, inviando cioé la luce con una frequenza estremamente bassa, il comportamento della luce era tipicamente particellare. Come poteva accadere ciò?
Semplicemente si doveva pensare alla luce come composta da particelle cui assegnare un particolare vettore che ne trasporta le caratteristiche salienti. Queste, interagendo con la materia, venivano opportunamente modificate: l'applicazione di modifiche successive e il quadrato del modulo del vettore risultante da queste applicazioni era in grado di spiegare le osservazioni sperimentali, tutto questo però portò all'abbandono di una spiegazione intuitiva dei fenomeni di interazione tra luce e materia e a un'interpretazione probabilistica e non deterministica dei fenomeni stessi.
E' questo, in sintesi, parte delle lezioni che Richard Feynman tenne all'UCLA agli inizi degli anni Ottanta del XX secolo all'interno di un programma di conferenze di divulgazione scientifica promosse dalla Fondazione Alix G. Mautner. Quelle quattro conferenze di Feynman vennero successivamente raccolte, trascritte e redatte con l'aiuto di Ralph Leighton per dare vita a QED - La strana teoria della luce e della materia, in cui il Premio Nobel racconta nel modo più semplice possibile, ma senza mai banalizzare, la teoria dell'elettrodinamica quantistica, che ha contribuito a migliorare e rendere quella che è oggi.

Nella tela del ragno

Carissimi amici nerd, uno dei nostri miti è sicuramente Peter Parker, meglio noto come l'Uomo Ragno. Ragazzino inteliggente, quasi geniale, venne punto da un ragno radiattivo ottenendone le caratteristiche, ma proporzionate ad un uomo. Una delle prime cose che il ragazzo pensò bene di fare fu cercare di realizzare una sostanza in grado di riprodurre le proprietà della tela di un ragno, in maniera da sostenerlo durante i suoi volteggi tra i palazzi di New York. In effetti, fin dagli anni Sessanta, quando il supereroe fu creato da Stan Lee e Steve Ditko, si sapeva che la seta prodotta dai ragni è più resistente dell'acciacio, ma oggi, dopo quaranta anni dagli esperimenti casalinghi di Peter, un gruppo di fisici tedeschi ha scoperto che può essere anche più forte aggiungendo piccole quantità di metallo.
La scoperta potrebbe aiutare i ricercatori a comprendere perché alcune strutture biologiche che contengono metalli, come mascelle e pungiglioni, sono così forti. Potrebbe anche condurre a nuovi processi per realizzare materiali naturali e artificiali più resistenti.
La seta del ragno è un polimero fatto con piccoli strati cristallini di proteine legate una con l'altra da reticoli amorfi di aminoacidi. I ragni producono differenti tipi di seta, ma Mato Knez e colleghi del Max Planck Institute of Microstructure Physics e dell'Università Martin Luther, hanno studiato un tipo particolare di tela, fatta di un materiale non appiccicoso che i ragni utilizzano per rinforzare e appendere le loro ragnatele.

Grafene: il più duttile del mondo

Fin dalla sua scoperta nel 2004, il grafene continua ad affascinare i fisici con la crescita della lista delle sue eccezionali proprietà elettriche e meccaniche. Mentre piccoli pezzi di materiale, che è uno strato di carbonio spesso appena un atomo, sono costruiti con semplicità, è più difficile realizzare campioni di grande qualità e grandi superfici che posono essere utilizzati in dispositivi al grafene.
Ora ricercatori francesi hanno realizzato con un processo semplice dei pezzi di grafene relativamente grandi. Abhay Shukla e colleghi dell'Università Pierre e Marie Curie mostrano che grandi quantità di grafite possono essere depositate sopra vetri di borosilicato e quindi spaccarsi per lasciare un singolo reticolo di grafene sul substrato.

L'uomo che sapeva troppo

---

Titolo: L'uomo che sapeva troppo
Autore: David Leavitt
Edizione: La biblioteca de Le Scienze

Giusto settanta anni fa la Germania invadeva la Polonia, dando così inizio alla Seconda Guerra Mondiale. Un ruolo particolare lo rivestiranno, sia da una parte sia dall'altra, proprio gli scienziati, e i migliori talenti dell'epoca verranno impiegati in molti campi, soprattutto nella scienza applicata. Ingegneri, fisici, ma anche matematici. Tra tutti spicca il nome di Alan Turing, oggi considerato uno dei padri del computer e sicuramente un anticipatore delle teorie e dei lavori alla base dell'intelligenza artificiale e delle reti neurali.
Nato il 23 giugno del 1912, Turing rappresenta, in un certo senso, un doppio smacco per la Germania di Hitler, considerando che lavorò e sconfisse la macchina Enigma, che tante vittorie sembrava dover dare ai tedeschi, ma soprattutto apparteneva a una delle tipologie di persone perseguitate dal suo regime: gli omosessuali.
Oggi, forse, in molti prenderebbero il computer e lo getterebbero dalla finestra, o magari si rifiuterebbero di usarlo o più semplicemente inizierebbero a negare il valore e il merito di Turing nella storia del computer e dell'intelligenza artificiale, eppure la dedizione del matematico britannico nello studio della logica applicata alle macchine per la creazione di una intelligenza artificiale che fosse paragonabile a quella umana è assodato per tutta la comunità scientifica. E il libro di David Leavitt è un percorso attraverso i suoi articoli, il suo lavoro sull'Enigma, i suoi molteplici interessi, estremamente rigoroso e preciso, a volte anche molto tecnico, ma che si riesce comunque a seguire, considerando quanto ostica è la materia di cui si è occupato Turing per la maggior parte della sua carriera scientifica.

L'ipotesi di Riemann

---

Titolo: L'ossessione dei
numeri primi
Autore: John Derbyshire
Edizione: La biblioteca de
Le Scienze

E proseguiamo con l'esame dell'Ipotesi di Rieman e del libro L'ossessione dei numeri primi.
Il tipo di ricerca che l'Ipotesi ha fatto partire, sui numeri primi e su quanto sono fitti, è in effetti iniziata più come un semplice gioco matematico, ma col tempo ha guadagnato un'importanza che va al di là del semplice diletto: senza considerare tutto quello che John Derbyshire ci propone nel testo, basti pensare al ruolo che i numeri primi hanno assunto nella crittografia: è proprio sui numeri primi che si basano molte delle chiavi di sicurezza più... sicure su internet.
Veniamo, finalmente, all'enunciato dell'Ipotesi:

Tutti gli zeri non banali della funzione zeta hanno parte reale 1/2

dove la zeta di Riemann è data dall'espressione: \[\zeta(s)=1+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\frac{1}{5^s}+\cdots\] dove la variabile è indicata con la lettera $s$ invece dell'usuale $x$ già nel saggio di Riemann di 150 anni fa, e da allora la consuetudine è rimasta. L'espressione può essere scritta in maniera più concisa, tenendo conto di ognuno degli infiniti termini, utilizzando la sommatoria: \[\zeta(s)=\sum_n n^{-s}\] dove la somma viene fatta da 1 all'infinito.

L'ossessione dei numeri primi

---

Titolo: L'ossessione dei
numeri primi
Autore: John Derbyshire
Edizione: La biblioteca de
Le Scienze

L'11 agosto del 1859 Bernhard Riemann venne nominato membro corrispondente dell'Accademia di Berlino: come d'uso a quell'epoca Riemann presentò un saggio su uno degli argomenti di ricerca che lo interessavano in quel momento.
Il lavoro, Sul numero dei primi minori di una certa grandezza, presentava quella che passò alla storia della matematica come l'Ipotesi di Riemann, anche se John Derbyshire ritiene sia più opportuno chiamare congettura, e che in pratica rivoluzionò questa scienza grazie ai tentativi di dimostrarla. Non dovevano, infatti, passare che 41 anni affinché David Hilbert, nel suo famoso discorso al congresso dei matematici di Parigi di inizio XX secolo, mise l'Ipotesi di Riemann tra i 23 problemi che la matematica avrebbe dovuto affrontare nel secolo successivo.
L'Ipotesi, famosa anche come l'8.o problema di Hilbert, non è a tutt'oggi stata dimostrata, eppure i tentativi per dimostrarla hanno portato a risultati eccezionali che hanno fatto avanzare la matematica: L'ossessione dei numeri primi, di Derbyshire, è la storia di questi tentativi e degli uomini che li hanno fatti.

Il diavoletto di Maxwell

Sin da quando James Clerk Maxwell immaginò il suo demone circa 150 anni fa, i fisici si sono divertiti nel cercare di creare questo malizioso diavoletto. L'ultimo tentativo è arrivato da un gruppo di ricercatori dell'Università dell'Oregon che hanno creato una serie di laser che ordinano un insieme di atomi ultrafreddi, proprio come l'ipotetico demone.
Maxwell immaginò il suo demone come una minusocla creatura che può controllare una botola in un gas per segregare gli atomi caldi da quelli freddi. Propose questo esperimento mentale poiché sembrava offrire un modo semplice di violare il secondo principio della termodinamica riducendo l'entropia in un sistema senza spendere energia.
L'opinione più diffusa è che il demone, così come è stato concepito da Maxwell, sarebbe impossibile da realizzare, principalmente perché, ordinando gli atomi, il demone dovrebbe aprire e chiudere la botola ad istanti ben precisi; per fare ciò egli dovrebbe essere in grado di conoscere posizione e velocità di ogni atomo in ogni momento, in evidente contrasto con il principio di Heisenberg.

In un certo senso, per ottenere tale conoscenza, il demone dovrebbe trasferire l'entropia del gas nel suo cervello

dice Daniel Steck, uno dei ricercatori del gruppo dell'Oregon.

I problemi di Hilbert

David Hilzbert

L'8 agosto del 1900 al Congresso internazionale dei matematici tenutosi a Parigi nella prestigiosa Sorbona David Hilbert fece un lungo intervento d'apertura dei lavori, indicando quelli che a suo parere dovevano essere i problemi più urgenti da risolvere nel corso del XX secolo.
A causa della lunghezza del suo discorso, parlò solo di 10 dei 23 problemi che aveva identificato: 1, 2, 6, 7, 8, 13, 16, 19, 21, e 22. La lista completa venne pubblicata successivamente tra gli atti del congresso. Con il suo discorso e l'indicazione dei problemi, Hilbert diede una linea di pensiero e di ricerca alla matematica del XX secolo, segnandone di fatto tutto il cammino. Di tutte le questioni indicate dal matematico di Gottinga, l'università dove insegnava, due restano ancora aperte: l'ipotesi di Riemann e l'estensione del teorema di Kronecker a campi algebrici arbitrari. Per altri 8 la risoluzione è stata parzialmente accettata, 4 sono troppo vaghi e generali, uno (la determinazione delle soluzioni generali di un'equazione diofantea) è irresolubile, un altro (per $a \not= 0,\, 1$ algebrico e $b$ irrazionale, $a^b$> è sempre trascendente) è risolto parzialmente, mentre i rimanenti sono tutti risolti.
Torniamo, però, al discorso di Hilbert leggendone alcuni passaggi:

Chi di noi non vorrebbe essere lieto di sollevare il velo dietro il quale il futuro rimane nascosto; di gettare un'occhiata ai prossimi avanzamenti della nostra scienza e ai segreti del suo sviluppo durante i secoli futuri? Quali particolari obiettivi ci saranno attraverso i quali gli spiriti guida della matematica delle future generazioni si ingegneranno? Quali nuovi metodi e nuovi fatti nell'ampio e ricco campo del pensiero matematico rivelerà il nuovo secolo?
La storia ci insegna la continuità dello sviluppo della scienza. Sappiamo che ogni era ha i suoi particolari problemi, che l'era seguente risolve o mette da parte come poco promettenti e li sostituisce con nuovi. Se otterremo un'idea del probabile sviluppo della conoscenza matematica nell'immediato futuro, dobbiamo lasciare che le domande insolute passino prima la nostra mente e guardare poi ai problemi che la scienza di oggi propone e la cui soluzione aspettiamo dal futuro. Una tale revisione dei problemi di oggi, giacenza al meeting del secolo, mi sembra quanto più adatta. La chiusura di una grande epoca non solo ci invita a guardare indietro nel passato ma anche a dirigere i nostri pensieri all'ignoto futuro.
Il profondo significato di alcuni problemi per l'avanzamento della scienza matematica in generale e il ruolo importante che giocano nel lavoro dei singoli ricercatori non deve essere negato. Quanto più una branca dela scienza offre un'abbondanza di problemi, tanto più a lungo vive; una mancanza di problemi prefigura l'estinzione o la cessazione dello sviluppo indipendente. Così come ogni uomo intraprendente persegue certi obiettivi, così anche la ricerca matematica richiede i suoi problemi. E' dalla soluzione dei problemi che l'investigatore testa la tempra del suo acciaio; egli cerca nuovi metodi e nuovi sguardi, e guadagna un più ampio e più libero orizzonte.

Ritratti: Neil Armstrong

Quel giorno, in tutto il mondo, si sentirono queste parole:

That's one small step for [a] man, one giant leap for mankind.⁽¹⁾

Queste furono le parole di Neil Armstrong il giorno in cui entrò nella storia, come il primo uomo che pose piede sulla Luna, il nostro lontano e affascinante satellite, giust'appunto 40 anni fa.
Nato il 5 agosto del 1930 (l'anno prossimo ne festeggeremo, quindi, gli 80 anni), Armstrong, che comandava la missione Apollo 11 che sarebbe atterrata sul suolo lunare, non era solo in quella notte eterna e brillante di stelle. Lo accompagnarono in quel lungo viaggio e infine nello sbarco Aldrin, che con lui condivideva il passato di scout, e Collins.
Armstrong può, in un certo senso, essere considerato predestinato: nel 1968 era a capo dell'equipaggio di riserva dell'Apollo 8 e nello stesso anno, a maggio, rischiò la vita durante un'esercitazione con un modulo lunare. Per sua e nostra fortuna fu in grado di salire sull'Apollo 11 e mettere, per primo, piede sul nostro satellite.
All'astronauta statunitense sono anche intitolati un piccolo cratere lunare e un asteroide, il 6469 Armstrong.

La matematica in gioco: Reticoli euleriani

In una serie dedicata a Eulero non poteva mancare un articolo dedicato ai reticoli (o cammini) euleriani. Prima di addentrarci nei labirintici percorsi euleriani, vi ricordo che è da pochi giorni on line il 15.mo Carnevale della Matematica: i nostri Rudi amici si occupano, tra le altre cose, del gioco del 15, un particolare quadrato magico ideato nel 1874 dal postino Noyes Palmer Chapman e diffuso nel 1880 da Samuel Loyd.
Torniamo, però, a noi.
Tutto inizia con il problema dei ponti di Königsberg: in questo famoso problema, il solutore deve cercare di trovare l'eventuale percorso che consenta di attraversare ogni ponte una e una sola volta e tornare, alla fine, al punto di partenza. Non solo Eulero determinò che non esisteva alcun percorso di questo genere, ma diede di fatto il via alla teoria dei grafi. In particolare si possono fornire una serie di definizioni che possono aiutare a determinare se un reticolo è euleriano o meno, ma che possono anche aiutare a seguire meglio il ragionamento per la risoluzione del 15.mo problema del Project Euler.

La matematica in gioco: Terne pitagoriche

E torniamo a giocare con la matematica (e con quale altra disciplina, o scienza, o follia della mente potreste mai pensare di divertirvi seriamente?). In questo caso ci occupiamo del famigerato teorema di Pitagora, quello dei triangoli rettangoli, dei quadrati costruiti sui suoi lati, due dei quali, quelli ad angolo retto, detti cateti, e l'ultimo detto ipotenusa. Certo Pitagora non pretende che vi mettiate a costruire dei quadrati sopra ai poveri cateti o magari sopra alla delicata ipotenusa, ma potreste farlo semplicemente con carta e penna e poi con il righello verificare che quel geniaccio aveva semplicemente ragione. O magari provare a ricavare un'espressione tipo questa: \[c_1^2 + c_2^2 = i^2\] Per questo e molti altri risultati possiamo dire che la scuola di Pitagora fu una delle più grandi scuole filosofico-matematiche dell'antichità. Molte delle osservazioni di Pitagora e dei suoi allievi, infatti, non solo vennero successivamente confermate (ad esempio la teoria eliocentrica, una delle festeggiate in questo splendente anno astronomico), ma anche col tempo riscoperte, come ad esempio proprio il teorema di Pitagora, dimostrato da Euclide nel primo volume degli Elementi.

Ritratti: Alfred Wallace

Alfred Wallace - via commons

Charles Darwin, di cui quest'anno ricorrono i 200 anni dalla nascita e i 150 dalla pubblicazione de L'origine della specie, non è stato l'unico ad avere idee evoluzioniste. Praticamente in contemporanea con lui, anche Alfred Russell Wallace sviluppò la sua versione dell'evoluzione.
Diversamente da quanto si possa pensare, non ci fu rivalità tra i due, né lotta per chi dovesse accaparrarsi la paternità della scoperta: semplicemente Wallace si piegò al lavoro di decenni di Darwin, tanto che inviò a quest'ultimo il suo famoso saggio del 1858 On the Tendency of Varieties to Depart Indefinitely From the Original Type: questo, insieme a On the Law Which Has Regulated the Introduction of New Species del 1855 e al libro Darwinism del 1889 coostituiscono i suoi contributi alla teoria dell'evoluzione.
Gli studiosi hanno trovato, comunque, alcune differenze tra le idee di Wallace e quelle di Darwin, nonostante quest'ultimo non le abbia rilevate. Innanzitutto Darwin pose l'accento essenzialmente sulla competizione tra individui della stessa specie nella lotta per la sopravvivenza e la riproduzione. Wallace, invece, sottolineò l'importanza dell'ambiente esterno come forza veicolante dell'adattamento delle specie esterne all'ambiente circostante.
Altri hanno invece sottolineato come le idee di Wallace in merito alla selezione naturale come meccanismo per mantenere l'adattamento delle specie all'ambiente esterno siano le più potenti e importanti mai uscite dal XIX secolo.

La matematica in gioco: Sul Carnevale della Matematica e il Project Euler

E giunse, puntuale come ogni mese, il 14.mo Carnevale della Matematica. Ospitato da Matematica 2005, questa volta, mi sembra, un po' in tono minore: sarà la primavera che se ne va, sarà il caldo che avanza, sarà l'antigelo che non funziona poi molto bene vista l'assenza del gelo, questa volta le segnalazioni sono pochine. D'altra parte prima o poi il 14.mo carnevale doveva arrivare e un po' tutti sembra si sono fatti trovare impreparati alla doppia ricorrenza.
Se facciamo una piccola ricerca sul 14, però, scopriamo alcune cose interessanti: innazitutto è il numero atomico del silicio, che è di casa in questi nostri lidi elettronici; quindi è il terzo numero quadrato piramidale: 14 = 1 + 4 + 9; è anche il numero massimo totale di giocatori che possono giocare una partita ufficiale di calcio.
Concentriamoci, però, sul numero piramidale, perché ci consentirà di risolvere il Problema n.6 del Project Euler. Il problema n.6 recita, più o meno, così:

La somma dei quadrati dei primi dieci numeri è 385, mentre il quadrato della somma dei primi dieci numeri è 3025.
Trovare la differenza tra il quadrato della somma e la somma dei quadrati dei primi 100 numeri.

I numeri piramidali quadrati fanno proprio al caso nostro: tali numeri sono definiti come la somma dei quadrati dei primi $n$ numeri interi: \[Q_n = \sum_{k=1}^n k^2 = \frac{n(n+1)(2n+1)}{6}\] Allora, utilizzando la formula per i numeri triangolari, già utilizzata per il Problema n.1, combinata con quella per i numeri piramidali quadrati otteniamo la risposta al nostro problema: \[R_{100} = T_{100}^2 - Q_{100}\] che risulta una soluzione molto elegante per il Problema n.6, che i più arguti di voi ricorderanno che vi avevo già proposto.
Ritornando al Carnevale, vi ricordo che per leggere l'elenco dei passati Carnevali e prenotarsi, fate riferimento a Matematti.
Alla prossima!

Il pendolo di Skoda

da un video di Miroslava Hajek

Nel 1583 Galileo Galilei scoprì l'isocronismo del pendolo. La leggenda vuole che Galilei ebbe l'intuizione osservando le oscillazioni di una lampada nella navata centrale del Duomo di Pisa. A quel punto ecco il pendolo, uno strumento semplicissimo costituito da una corda e da un pesetto legato a un capo del filo, mentre l'altro viene fissato.
Il pendolo è però uno strumento complesso da studiare ed è possibile trovare una soluzione semplice al problema, la periodicità delle oscillazioni, solo se si fa l'approssimazione delle piccole oscillazioni.
In questo caso la legge per calcolare il periodo è data dall'equazione: \[T = 2 \pi \sqrt{\frac{l}{g}}\] dove $T$ è il periodo di oscillazione, $l$ la lunghezza del filo e $g$ l'accelerazione di gravità.
Come si può notare il periodo di oscillazione non dipende dalla massa del pesetto, ma solo dalla lunghezza del filo: questa equazione può essere determinata con dei calcoli o nello stesso modo con cui la scoprì Galileo (anche se per scriverla non usò lo stesso simbolismo, ma la descrisse a parole), ovvero con dei semplici esperimenti.

Archeologia astronomica

La nebulosa del granchio (via commons)

Il 1609 fu un anno magico per l'astronomia, ma questo ormai si sa: Galileo Galilei e Johannes Keplerrivoluzionarono lo studio dei cieli e la comprensione del moto dei pianeti con osservazioni accurate come mai prima (Galilei) e calcoli e leggi ancora oggi validi (Kepler). Tutto nasceva dall'osservazione delle supernove: fu proprio una di queste, nel 1604, che fece interessare Galilei del cielo, e furono quelle del 1609 che spinsero i due scienziati, separatamente, ad occuparsi di misteri fino a quel momento affidati alla religione e ai filosofi aristotelici.
Di eventi di questo genere (esplosioni in cui la stella esplodente espelle parte della sua massa, cambiando in molti casi anche la sua stessa densità) nella storia dell'universo ce ne sono quante le stelle nel cielo, e alcuni di questi sono stati registrati anche prima dell'era di Galileo: ad esempio nella primavera del 1006, gli astronomi osservarono quella che si può definire come la più brillante supernova ricordata nella storia. Giusto 48 anni dopo una nuova supernova nella Nebulosa del Granchio: la nostra attuale conoscenza di questi eventi del passato è basata sui calcoli di astronomi cinesi e arabi, passando per le osservazioni moderne dei resti delle supernove.